CIENTISTAS QUESTIONAM O "TEOREMA DE PITÁGORAS"

 Durante uma reunião seccional da Sociedade Americana de Matemática (AMS) em 18 de março, as estudantes apresentaram suas descobertas. Uma delas forneceu entrevista, e disse que o sentimento é indescritível. Afinal, elas conseguiram realizar algo que muitos acreditaram não ser possível, e profissionais não conseguiram fazer.

Via Wikimedia

Sobre o Teorema de Pitágoras

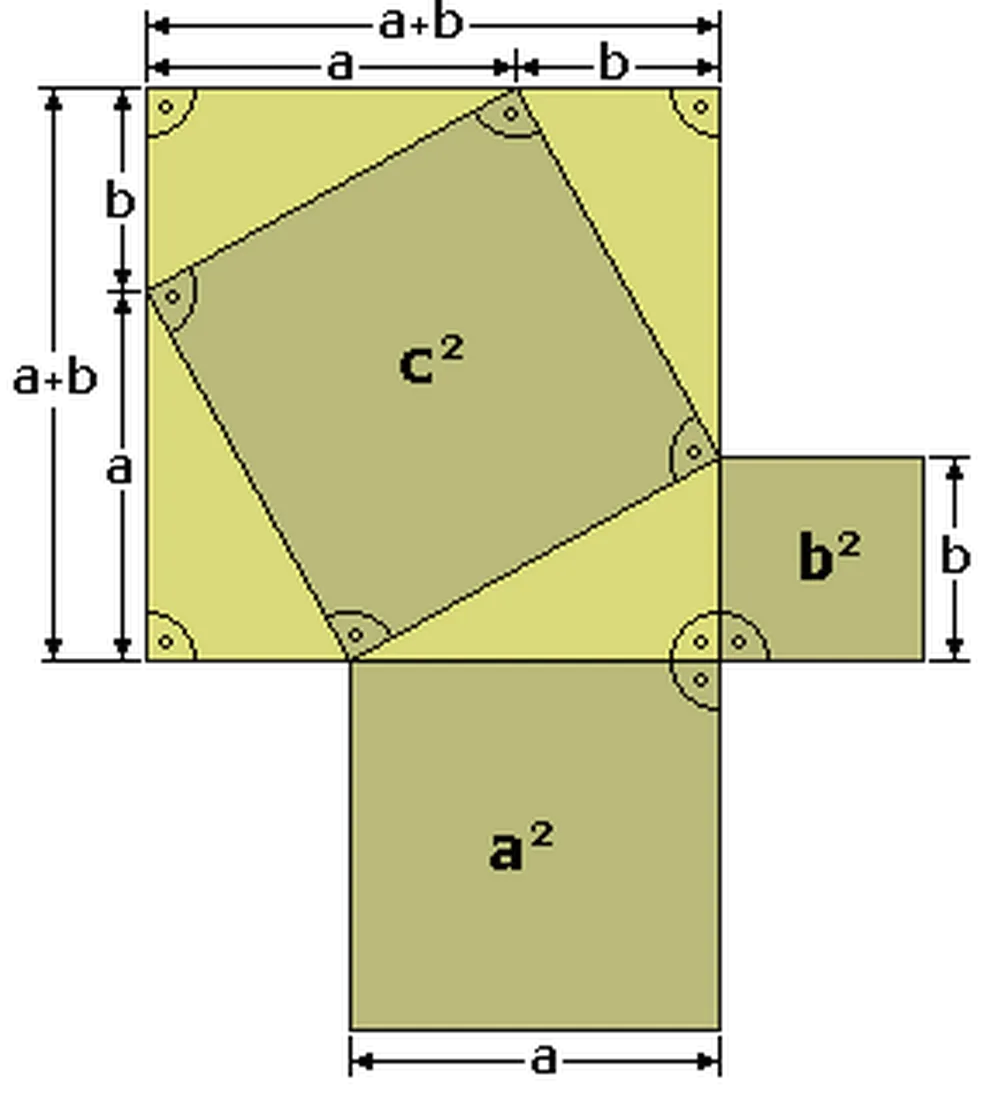
Há cerca de 2 mil anos, surgiu o Teorema de Pitágoras, afirmando que a soma dos quadrados dos dois catetos de um triângulo retângulo é igual ao quadrado da hipotenusa.

Esse teorema é a base da trigonometria, que vem das palavras gregas para “triângulo” (trigonon) e “medir” (metron). Essa área da matemática estabelece a relação entre os comprimentos laterais e os ângulos de um triângulo.

No entanto, matemáticos sempre pensaram que 

usar a trigonometria para provar o teorema 

seria uma falha lógica conhecida como 

raciocínio circular. Isso porque as fórmulas 

fundamentais da trigonometria são baseadas 

na verdade do Teorema de Pitágoras, como 

afirmou o matemático estadunidense Elisha 

Loomis (1852-1940) em seu livro “The 

Pythagore acreditam que isso não é verdade. Em seu artigo, elas apresentam uma nova prova do Teorema de Pitágoras que se baseia na Lei dos Senos.

Esse é um resultado fundamental da trigonometria, e mostra que a prova é independente da identidade trigonométrica pitagórica \sen^2x + \cos^2x = 1. Essa descoberta pode ter implicações significativas para o campo da matemática e é digna de nota.

Incomum

Segundo o Live Science, Scott Turner, diretor de comunicações da AMS, afirmou que não é comum que estudantes do ensino médio apresentem em uma Reunião Seccional da AMS.

Além disso, Catherine Roberts, diretora-executiva da AMS, explicou que, após a apresentação na conferência, o próximo passo seria enviar o trabalho delas para um periódico com revisão por pares.

Com isso, membros da comunidade de matemática podem examinar seus resultados para determinar se sua prova é uma contribuição correta para a literatura matemática.

Embora seja muito cedo para determinar se Calcea e Ne’Kiya realmente vão revolucionar esse campo da ciência, é certo que elas têm um futuro promissor pela frente.

Como se prova uma teoria matemática?

Provar uma teoria matemática envolve mostrar que uma afirmação é verdadeira em todas as situações possíveis.

Geralmente, a prova é baseada em um conjunto de axiomas, ou postulados, que são considerados verdadeiros sem necessidade de prova.

A partir desses axiomas, são usados os princípios da lógica e da dedução para chegar a uma conclusão lógica.

Existem diferentes técnicas para provar teorias matemáticas, que variam de acordo com a complexidade do problema.

Algumas dessas técnicas incluem: prova direta, prova por contradição, prova por indução matemática, prova por construção, prova por casos, entre outras.

Independentemente da técnica utilizada, uma prova matemática deve seguir uma estrutura lógica clara e coerente, com todas as etapas de raciocínio e cálculo explicadas em detalhes. A prova deve ser revisada e validada por outros matemáticos para garantir que seja completa e correta. Essa execução é mais complexa quando se trata de teorias antigas. Isso porque elas são a base do que entendemos como matemática. Ou seja, não é possível usar as fórmulas base para provar as teorias base. No entanto, as estudantes mostraram que essa possibilidade existe, abrindo novas alternativas para os próximos estudiosos. Resta comprovar se é real o resultado, e qual seu impacto no entendimento trigonométrico.

 

Fonte: Revista Galileu

Imagens: Globo, Wikimedia